How the Pipe Produces Sound?

Frost quickly coats the cold part of the pipe

Let the pipe heat up and let us look at its mystery.

Basically, the thermoacoustic pipe is a tube which is closed on one end. Suppose that the air in it oscillates at the fundamental frequency like in the simple tube closed at one end. This is an approximation since the thermoacoustic pipe is not an empty tube and the temperature along the pipe is not constant. The air in the empty tube is compressed toward the closed end and expanded toward the opening while the tube 'sings'. So the air in the tube oscillates along the tube and is compressed while moving toward the closed end and expanded while moving toward the open end.

Oscillation of the air at a fundamental frequency in the half-closed empty tube

Click on the figure to see animation.
(51 k)

Let us orientate the thermoacoustic pipe with the closed end to the right like the tube on the upper figure. Any chosen volume of air in the pipe is then compressed while moving to the right and expanded while moving to the left. Because the movements are swift (the frequency of the oscillation is 200 Hz in our case) the compression and expansion are adiabatic. So the air heats up (red color on the figure) while being compressed and cools while being expanded.

The plastic part of the pipe is densely perforated with small holes. Let us limit ourselves to only one little hole and look closely at what is going on in a region close to the hole wall.

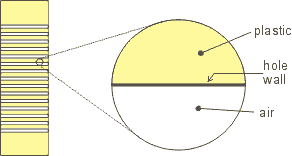Temperature of the wall changes along the hole. The right end of the plastic part is warmer than the left one because the right end is joined with the copper part of the pipe we hold in our hand while the left end is joined with the copper part cooled in liquid nitrogen. We shall assume that the temperature of the plastic wall rises linearly to the right.

Let us choose a small volume of air close to the hole wall and follow its path along the wall. The chosen volume should be large enough so that its thermodinamical description is valid. Let us name the chosen volume of gas 'a parcel of gas'.

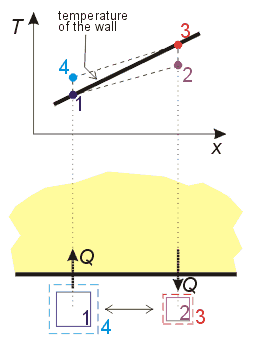
The figure on the right shows the wall temperature depending on the x coordinate along the hole. We limit ourselves to the region of coordinate x in which our gas parcel oscillates.

We start with our parcel at the point 1. Its temperature is equal to the temperature of the adjacent wall. For the sake of simplicity we shall replace parcel's sinusoidal motion with the rectangular one: rapid motion - wait - rapid motion - wait - etc. So the parcel rapidly moves to the point 2. Its temperature increased because during the movement it compressed adiabatically. Still its temperature is lower than that of the adjacent wall (look at the temperature diagram) and during the wait period the parcel accepts heat Q from the wall. Parcel's temperature rises until it equals the temperature of the wall (point 3). During the isobaric heating (2-3) parcel expands as indicated on the figure. In the next step the parcel rapidly moves back to the starting point (4). Because it accepted heat in step 2-3, its temperature is higher than that of the adjacent wall. Therefore the parcel gives heat Q to the wall and cools to the temperature of the adjacent wall (point 1). Parcel's volume is reduced due to isobaric cooling.

In the cycle described above, the parcel carried heat Q from the hole wall with the higher temperature to the wall with the lower temperature.

Temperature of the parcel which oscillates along the wall

p-V diagram of parcel's thermodynamical cycle

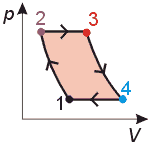
The thermodynamic cycle of the parcel is described with two adiabatic curves (1-2 and 3-4) and two isobaric curves (2-3 and 4-1). The area the cycle encloses in the pressure-volume diagram equals the work released in the cycle. In our case the work is done on the parcel.

During the time of one cycle, the parcel carries heat Q from a place with higher temperature to the place with lower temperature and receives work (work is done on the parcel).

The same holds for all parcels which are suitably close to the hole wall in the plastic part of the pipe. They receive work and transport heat to the left. We could imagine that the heat Q a parcel transported in a cycle is carried forth by his neighbouring parcel in next cycle. In one cycle they altogether carry heat Q from the right (warm) copper part to the left (cold) copper part. Heat transport stops in a copper section beacause the temperature of the copper does not change along the coordinate x due to copper's big thermal conductivity.

Parcels carrying heat along the hole wall

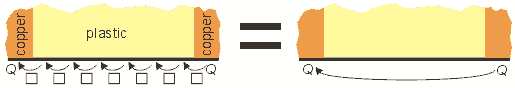
The work the parcels receive manifests as an increase of the acuostic energy of the pipe. As the pipe 'sings' the acoustic energy is radiated away. The pipe would quickly stop emitting sound if the energy wouldn't be replaced. The lost energy is replaced by the work the parcels receive.

Termoacoustic effect takes place in a fluid (in our case air) which oscillates like a gas in a simple tube at its fundamental frequency and suitably close to the wall, the temperature of which changes along the path of the oscillating fluid (it rises in the direction of motion of the fluid as its pressure increases). The fluid carries heat from the hotter part of the wall to the colder part of the wall and the acoustic energy of the fluid increases.

Now we can explain why the middle part of the pipe is made of plastics and the other two of copper. We already explained the importance of changing temperature along the plastic part. We obtain it dipping the open copper part of the pipe in liquid nitrogen and holding the other copper part with a bare hand. The temperature of the open end is very low and constant throughout the copper part due to copper's big thermal conductivity. The other copper part is kept warm with the hand. The plastic part is in touch with the cold copper part on the left and the warm copper part on the right. Because plastics is rather poor thermal conductor the part's left side is cold and its temperature increases to the warm right side. That is how we obtain one of the above conditions for the existence of the thermoacoustic effect.

But how can we obtain the required oscillation of the fluid? If the air in the pipe would be completely still nothing interesting would happen. Heat would slowly flow through the plastic part and the temperatures of the copper parts would equalize after some time. But the air is never completely still. Normally, there is a lot of noise coming from traffic, computers in operation, opening and closing doors, talking, etc. The pipe being an acoustical resonator picks up its frequency out of the existing noise. As soon the air in the pipe begins to oscillate the thermoacoustic effect amplifies the oscillations and the pipe begins to 'sing'.

When does the pipe stop emitting sound? The oscillating air in the plastic part transports heat and therefore actively heats up the cold copper part of the pipe. The temperature of the warm copper part is kept constant using the hand as a thermal reservoir. The slope of the wall temperature on the diagram above is therefore less and less steep. The point 4 moves toward the point 1 and the point 3 towards the point 2. When they come together the work received by the air drops to zero (compare with the pV diagram) and the pipe stops singing. The heat flowing through the plastics is considered as a loss and shortens the time of sound emission.

Now you can try to answer some interesting questions:

Would the pipe sing differently if the middle part was made of stainless steel instead of plastics?
Why do we use paper washers?
How would we obtain louder sound?
What would happen if we would cool the closed part and hold the open part of the pipe? Would the pipe sing?
What if we would hold the open part and heat the closed part of the pipe? (Assume the pipe is heat resistant.)
What is the difference between the thermodynamical cycles of the parcels very close to the wall, far away from the wall and the parcels between them?
Why does the frequency and amplitude of the emitted sound change with time?

Let me recommend you an article with wich you will be able to answer all the above questions except... Well, can you think of a good answer to the last question?

Easy to understand article with beautiful pictures:
G.W. Swift: Thermoacoustic engines and refrigerators, Physics Today, July 1995, 22,

Very thorough work on thermoacoustic engines:
G.W. Swift: Thermoacoustic engines, J. Acoust. Soc. Am. 84 (1988) 1145,

The pipe presented has been made after:
J. Wheatley, T. Hofler, G.W. Swift, A. Migliori: Understanding some simple phenomena in thermoacoustics with applications to acoustical heat engines, Am. J. Phys. 53 (1985) 147.

The House of Experiments The House of Experiments - hands-on science center in Ljubljana